三角形の合同はルールを守るだけ
三角形の合同は、皆さんが初めて直面する、証明問題です。
整数などでも簡単な証明は実は出題されていますが、証明として形式も含めてはじめて習うのがこの分野。
一般的な公立中学では2年生の後半か、3年生の最初に習いますが、中高一貫校では、中2の前半に習うことが多いです。
証明の重要性
高校受験する学生は、必ずこの場で身につけなければいけません。
高校受験の数学では証明に関連する問題がほぼ100%出題されます。
この先いくつか証明が出てきますが、三角形の合同はその基礎。
ここがわからなければ非常に苦労します。
実際に都立高校入試でも、埼玉県公立入試でも図形の証明問題は毎年出題されています。
定期テストでも非常に重要。
これから、
普通の三角形の合同→直角三角形の合同→三角形の相似→平行四辺形(長方形、ひし形、正方形も含む)と、4つの分野で証明が必要とされます。
つまり、三角形の合同証明が身につけば、これから2~4か月程度は数学が理解しやすく、
身につかなければ数学が一気にわからなくなります。
よくある質問は → こちら
作図も得意に
三角形の合同条件を理解することで、実は作図の理解にも役立ちます。
高校入試で高確率で出題される作図が、合同の理解で有利になります。
また、円と三角形、円と四角形という考え方は、高校でも非常に多く出題。
逆にこの分野をあやふやなままにすると、高校に入った後にも非常に苦労することになります。
さらに、作図も高校入試ではほぼ確実に出題されるので、入試対策にもなります。
証明に必要な4要素
証明には、
- 定義の理解
- 形式を身に着ける
- 基礎問題を解く
- 応用問題(複合問題)を解く
の4つのステップが求められます。
最重要は定義の理解
3つの合同条件を単純に暗記するだけではなく、きちんと意味を理解する必要があります。
単純暗記だけでも学校の定期試験はある程度はなんとかなりますが、偏差値55以上の高校入試であったり、高校入学後に理系を目指すことが決まっているのであれば、実感を持って理解しましょう。
さらにこの3つの定義は、相似を勉強するときや、直角三角形を勉強するときにも非常に役立ちます。
実感を持った理解には、自分で書いてみるのが一番です。
「3組の辺(の長さ)がそれぞれ等しい」
これを確認するためには、長さの違う3つの棒を用意して確かめてみて下さい。
その3本で、実際に三角形を作ってみて下さい。
試すとわかりますが、1種類しか三角形は作れません。
是非、長さも変えて試してみましょう。
適度なものがなければ、紙に書いてみるのも有効です。

「2組の辺(の長さ)と、その間の角がそれぞれ等しい」
2つの長さが固定された棒(鉛筆などでOK)を、間の角度を固定して置いてみて下さい。

あとは、空いているところをつなぐしか、選択肢がないはずです。
「1組の辺(の長さ)と、その両端の角がそれぞれ等しい」

紙の上に、長さが固定された棒を置いてください
これらの定義に関しても実際に書くとよく理解ができます。

定義の意味をしっかり理解しようと思うと、国語力が非常に重要なことがわかります。
国語(現代文)力は、数学においても文章題で非常に高い効果があります。
形式を身に着けるには、形式理解が必須
合同条件の形式はシンプルです。
例えば2つの三角形が合同であることを証明するためには、
3辺の長さが等しいことを証明する必要があります。
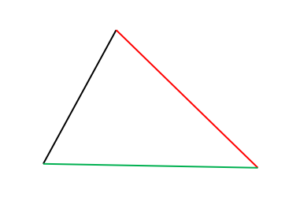
つまり、
赤の線の長さが等しい…①
黒の線の長さが等しい…②
緑の線の長さが等しい…③
ということを示します。
この①~③を示すには、そもそも問題文の条件に書いてあったり(仮定)、正三角形の一部の辺であったり(正三角形はすべての辺の長さが等しい)、と問題をしっかり読んで、そこから条件を見つけ出していくことになります。
そして3つの条件が成立することを書ければ、
①~③より、
「3組の辺(の長さ)がそれぞれ等しい」
ということがいえるわけです。
このように、どの辺とどの辺の長さが等しいのか、どの角度とどの角度が等しいのか、しっかり示すことで合同証明に必要なパーツを3つ集めます。
その3つを最後にまとめて記載することで合同の証明が完了となります。
実例で形式を理解しよう
では、次のようにA、B、C、Dという4つの点で作られた2つの三角形が合同であることを示してみましょう。
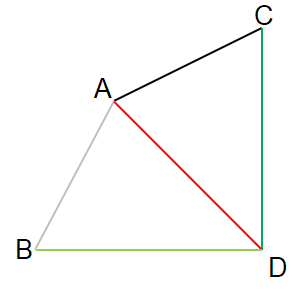
問題の条件として
AB=AC、BD=CDは、自由に使ってよいとします。
また、「△」の記号は「三角形」という意味であり、△ABCとは、A,B,Cの3点を頂点に持つ三角形を表現しています。
「≡」は「≡」という表現で、
「△ABC≡△DEF」と記載すると、三角形ABCと三角形DEFが合同であることを表現していることになります。
解答
△ABDと△ACDについて
(まずはどの部分に関する話なのかを、採点する人に示します。)
仮定より
AB=AC … ①
(仮定より、とは問題文に書いている条件です、ということです。)
仮定より
BD=CD … ②
(BDに対してはDCではなく、CDと書く必要があります。)
ADは共通 … ③
(2つの三角形において、共通の辺なので、長さが同じです、と示したことになります。)
(①、②、③が合同を示すための必要なパーツになっています。)
①~③より、
3組の辺(の長さ)がそれぞれ等しい ので、
(ここで合同条件を使いました。①~③のパーツを使いました、と明記する必要があります)
△ABD≡△ACD となる。
(これで証明は終了です。)
大切なのは、合同条件のために3つのパーツを集めてくること。
そして、どの合同条件を使ったのか明記することです。
最初は少しわかりにくいでしょう。
基本問題をこなしていくことで、形式に慣れます。
ある程度形式を覚えたらどんどん数をこなしましょう。
逆に、形式をあまり覚えない状態で問題を解いても非効率です。
基本さえ理解できれば、応用問題はそこまで難しくありません。
理解して、パターンをトレーニングしていきましょう。
数学の理解力を高めて点数アップするなら → こちら